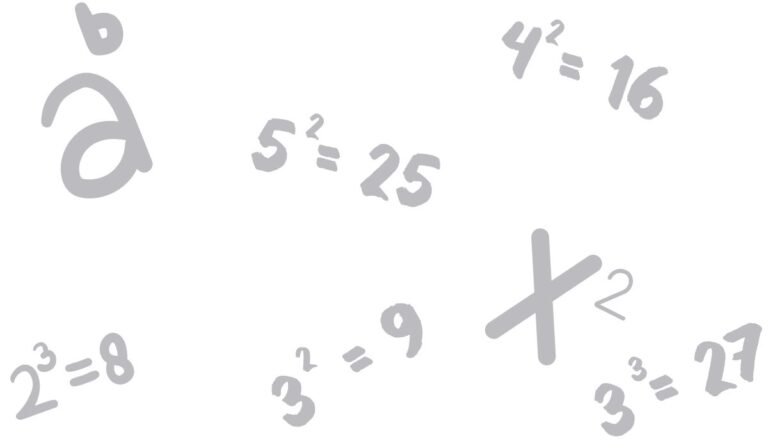Rangkuman Materi dan Soal Latihan Bentuk Pangkat

Bentuk pangkat adalah salah satu bentuk penulisan matematika untuk menyatakan perkalian berulang dari suatu bilangan atau variabel dengan dirinya sendiri. Notasi ini membuat penulisan lebih singkat dan mudah dibaca, terutama untuk bilangan yang dikalikan banyak kali.

Penulisan bentuk pangkat secara umum:
\( a^n = \underbrace{a \times a \times \dots \times a}_{n\ \text{faktor}} \)
Keterangan:
– \(a\) = bilangan pokok (basis)
– \(n\) = pangkat (eksponen), yaitu jumlah faktor perkalian

Contoh Bentuk Pangkat:

1. \(2^4 = 2 \times 2 \times 2 \times 2 = 16\)
2. \(5^3 = 5 \times 5 \times 5 = 125\)
3. \(x^5 = x \times x \times x \times x \times x\)
4. \(\left(\dfrac{3}{4}\right)^2 = \dfrac{3}{4} \times \dfrac{3}{4} = \dfrac{9}{16}\)
5. \(\left(-7\right)^3 = (-7) \times (-7) \times (-7) = -343\)
6. \(-7^3 = – (7 \times 7 \times 7) = -343\)

Fungsi dan Kegunaan Bentuk Pangkat

Bentuk pangkat sering digunakan dalam kehidupan sehari-hari, khususnya dalam sains dan teknologi, seperti:

• Menyederhanakan penulisan bilangan besar atau kecil, misalnya:
  • Jarak dari bumi ke matahari: \(1.496 \times 10^8\) km
  • Ukuran partikel mikroskopis: \(2 \times 10^{-6}\) meter
• Mempermudah perhitungan yang melibatkan bilangan berulang

Aturan Operasi Bentuk Pangkat

Ada beberapa aturan penting dalam operasi bentuk pangkat yang perlu diketahui:

1. \(a^m \times a^n = a^{m+n}\)
2. \(\dfrac{a^m}{a^n} = a^{m-n},\ a \neq 0\)
3. \((a^m)^n = a^{m \times n}\)
4. \(a^0 = 1,\ a \neq 0\)
5. \(a^{-n} = \dfrac{1}{a^n},\ a \neq 0\)
6. \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
7. \(a^1 = a\)

Catatan Penting

Perhatikan penulisan tanda kurung dalam bentuk pangkat. Misalnya:

• \((-3)^2 = 9\) karena \((-3) \times (-3) = 9\)
• \(-3^2 = – (3 \times 3) = -9\)

Penutup

Memahami bentuk pangkat adalah dasar penting dalam aljabar, terutama saat belajar tentang bilangan berpangkat, akar, dan logaritma. Dengan menguasai konsep ini, Anda bisa menyederhanakan banyak perhitungan matematika.

Selanjutnya, silakan coba kerjakan beberapa latihan soal tentang bentuk pangkat untuk memperdalam pemahaman.

Soal Latihan

1. Nilai \(x\) yang memenuhi \(\dfrac{2^{x}}{4^{x+2}}=16 \cdot 4^{x}\) adalah\(\cdots\)
   1. \(-3\)
   2. \(-\dfrac{8}{3}\)
   3. \(-2\)
   4. \(-\dfrac{4}{3}\)
   5. \(-\dfrac{2}{3}\)
2. Jika \(f(x)=b^{x}\), \(b\) konstanta positif, maka \(\dfrac{f(x^{2}-1)}{f(1-x^{2})}=\cdots\)
   1. \(f(1-x^{2}) \cdot f(1-x^{2})\)
   2. \(f(1-x^{2}) \cdot f(x^{2}-1)\)
   3. \(f(x^{2}-1) \cdot f(x^{2}-1)\)
   4. \(f(1-x^{2}) + f(1-x^{2})\)
   5. \(f(x^{2}-1) + f(x^{2}-1)\)
3. Nilai \(x\) yang memenuhi persamaan \(3^{2x+3}=\sqrt[3]{27^{x+5}}\) adalah\(\cdots\)
   1. \(-2\)
   2. \(-1\)
   3. \(0\)
   4. \(1\)
   5. \(2\)
4. Jika \(4^{x}-4^{x-1}=6\) maka \((2x)^x\) sama dengan
   1. \(3\)
   2. \(3\sqrt{3}\)
   3. \(9\)
   4. \(9\sqrt{3}\)
   5. \(27\)
5. Jika \(9^{m-1}+9^{m+1}=82\), maka \(4^{m+1}=\cdots\)
   1. \(\dfrac{1}{16}\)
   2. \(\dfrac{1}{4}\)
   3. \(4\)
   4. \(16\)
   5. \(64\)
6. Nilai \(1-x\) yang memenuhi persamaan \(\sqrt{8^{3-x}}=4 \cdot 2^{1-2x}\) adalah…
   1. \(-4\)
   2. \(-3\)
   3. \(-2\)
   4. \(3\)
   5. \(4\)
7. \(\dfrac{5^{4022}-5^{4018}}{5^{4020}-5^{4016}}=\cdots\)
   1. \(1\)
   2. \(3\)
   3. \(\dfrac{25}{4}\)
   4. \(\dfrac{25}{2}\)
   5. \(25\)
8. Jika \(A^{2x}=2\), maka \(\dfrac{A^{5x}-A^{-5x}}{A^{3x}+A^{-3x}}=\cdots\)
   1. \(\dfrac{31}{18}\)
   2. \(\dfrac{31}{9}\)
   3. \(\dfrac{32}{18}\)
   4. \(\dfrac{33}{9}\)
   5. \(\dfrac{33}{18}\)
9. Jika \(2^{(x+2)}+4^{(x+1)}=48\) nilai dari \(\dfrac{1}{x+1} =\cdots\)
   1. \({ }^3\!\log 2\)
   2. \(\dfrac{1}{14}\)
   3. \({ }^2\!\log 3\)
   4. \({ }^2\!\log 6\)
   5. \(3\)
10. Jika \(8^{m}=27\), maka \(2^{m+2}+4^{m}=\cdots\)
    1. \(12\)
    2. \(15\)
    3. \(18\)
    4. \(21\)
    5. \(24\)
11. Jika \(x_{1}\) dan \(x_{2}\) memenuhi \(2^{x^{2}}\ 4^{-2x}=\dfrac{1}{8}\) dengan \(x_{1} \gt x_{2}\), maka \(x_{1}-x_{2}=\cdots\)
    1. \(1\)
    2. \(2\)
    3. \(3\)
    4. \(4\)
    5. \(5\)
12. Jika \(f(x)=2^{2x}+2^{x+1}-3\) dan \(g(x)=2^{x}+3\) maka \(\dfrac{f(x)}{g(x)}=\cdots\)
    1. \(2^{x}+3\)
    2. \(2^{x}+1\)
    3. \(2^{x}\)
    4. \(2^{x}-1\)
    5. \(2^{x}-3\)
13. Solusi persamaan \(5^{2x+1}=10^{2x-1}\) adalah…
    1. \({}^2\!\log 25\)
    2. \({}^2\!\log 50\)
    3. \({}^4\!\log 25\)
    4. \({}^4\!\log 50\)
    5. \({}^5\!\log 4\)
14. Bila \(x=36\) dan \(y=125\) maka nilai \( \dfrac{x^{-\frac{3}{2}}\ { \sqrt[3]{y^{2}}}}{y^{\frac{1}{3}} – x^{\frac{1}{2}}} =\cdots\)
    1. \(-\dfrac{16}{216}\)
    2. \(-\dfrac{25}{216}\)
    3. \(-\dfrac{36}{216}\)
    4. \(-\dfrac{49}{216}\)
    5. \(-\dfrac{64}{216}\)
15. Jika \(n\) memenuhi \(\underset{n\ faktor}{\underbrace{25^{0.25} \times 25^{0.25}\times \cdots \times 25^{0.25}\times 25^{0.25}}=125}\)
    maka \((n-3)(n+2)=\cdots\)
    1. \(24\)
    2. \(26\)
    3. \(28\)
    4. \(32\)
    5. \(36\)
16. Jika \(4^{x}+4^{-x}=7\), maka nilai \(8^{x}+8^{-x} =\cdots\)
    1. \(14\)
    2. \(18\)
    3. \(27\)
    4. \(49\)
    5. \(81\)
17. Diketahui \(m,\ n,\) dan \(k\) adalah bilangan real sehingga mememenuhi sistem persamaan \(\begin{cases}\sqrt{5^{m-2n-k}} =25 \\ 25^{n+k} = 5 \end{cases}\)
    Nilai dari \(\dfrac{5^{m}}{5^{n}}=\cdots\)
    1. \(\sqrt{5}\)
    2. \(5\sqrt{5}\)
    3. \(25\sqrt{5}\)
    4. \(125\sqrt{5}\)
    5. \(625\sqrt{5}\)
18. Jika \(a\) dan \(b\) adalah bilangan bulat positif yang memenuhi \(a^{b}=2^{20}-2^{19}\), maka nilai \(a+b\) adalah…
    1. \(3\)
    2. \(7\)
    3. \(19\)
    4. \(21\)
    5. \(23\)
19. Jika \(3^{(1-2x)}-2 \cdot 3^{(2-2x)}+20 \cdot 3^{(1-x)}-5 \cdot 3^{2} =0\), hasil kali dari semua nilai \(x\) yang memenuhi persamaan tersebut adalah…
    1. \(-3\)
    2. \(-1\)
    3. \(0\)
    4. \(2\)
    5. \(3\)
20. Jika \(\dfrac{2^{\frac{1}{2}}+2^{\frac{1}{3}}}{2^{-\frac{1}{2}}+2^{-\frac{1}{3}}}=4^{x}\), maka \(x=\cdots\)
    1. \(\dfrac{1}{3}\)
    2. \(\dfrac{5}{12}\)
    3. \(\dfrac{1}{2}\)
    4. \(\dfrac{7}{12}\)
    5. \(\dfrac{2}{3}\)
21. Jika \(\sqrt[3]{4^{x+1}}=2\sqrt{8^{x}}\) maka nilai \(x=\cdots\)
    1. \(1\)
    2. \(\dfrac{2}{5}\)
    3. \(\dfrac{1}{5}\)
    4. \(-\dfrac{1}{5}\)
    5. \(-\dfrac{2}{5}\)
22. Bentuk sederhana dari
    \(\dfrac{\left (x^{\frac{1}{3}}-x^{\frac{1}{6}} \right )\left (x^{\frac{1}{2}}+x \right )\left (x^{\frac{1}{2}}+x^{\frac{1}{3}}+x^{\frac{2}{3}} \right )}{\left (x^{\frac{4}{3}}-x \right )\left (x+x^{\frac{1}{3}}+x^{\frac{2}{3}} \right )}\) dengan \(x \neq 0\) adalah…
    1. \(x^{-\frac{1}{3}}\)
    2. \(x^{\frac{1}{3}}\)
    3. \(x^{\frac{2}{3}}\)
    4. \(x^{-\frac{2}{3}}\)
    5. \(x^{\frac{1}{2}}\)
23. \(\dfrac{2015^{2}(2014^{2}-2013)}{(2014^{2}-1)(2014^{3}+1)}\times \dfrac{2013^{2}(2014^{2}+2015)}{(2014^{3}-1)}=\cdots\)
    1. \(2013 \times 2015\)
    2. \(2015\)
    3. \(2014\)
    4. \(2013\)
    5. \(1\)
24. Diketahui bahwa \(2^{w} \cdot a^{x} \cdot b^{y} \cdot c^{z}=2013\) untuk setiap \(a,b,c,d,x,y,z\) merupakan bilangan bulat positif dan \(w\) bilangan bulat nonnegative dengan \(a \lt b \lt c\). Nilai \((2w)+(ax)+(by)+(cz)=\ldots\)
    1. \(0\)
    2. \(3\)
    3. \(11\)
    4. \(75\)
    5. \(611\)
25. Jika \(a^{x}=b^{y}=c^{z}\) dan \(b^{2}=ac\), maka \(x=\cdots\)
    1. \(\dfrac{2yz}{y+z}\)
    2. \(\dfrac{2yz}{2z-y}\)
    3. \(\dfrac{2yz}{2y-z}\)
    4. \(\dfrac{yz}{2y-z}\)
    5. \(\dfrac{yz}{2z-y}\)
26. Jika \(x=\left(p^{-\frac{1}{2}}-q^{-\frac{1}{2}} \right)\left(p^{-1}+q^{-1}+2 \left( pq \right)^{-\frac{1}{2}} \right)^{\frac{1}{2}}\) dan \(y=\left(p+q \right)^{-2} \left(p^{-1}+q^{-1} \right)\) dengan \(p,q \gt 0\), \(p \neq q\), maka \(\frac{x}{y}=\cdots\)
    1. \(\left(p +q \right)^{-1}\)
    2. \(\left(p +q \right)^{-2}\)
    3. \(\left(p +q \right)^{2}\)
    4. \(\sqrt{p} + \sqrt{q}\)
    5. \(\sqrt{p} – \sqrt{q}\)
27. Jika \(x\) dan \(y\) adalah bilangan real dengan \(x \gt 1\) dan \(y \gt 0\). Jika \(xy=x^{y}\) dan \(\dfrac{x}{y}=x^{5y}\), maka \(x^{2}+3y=\cdots\)
    1. \(29\)
    2. \(28\)
    3. \(27\)
    4. \(26\)
    5. \(25\)
28. Jika \(4^{x}+4^{-x}-2^{2-x}+2^{2+x}-7 = 0\), dengan \( x \gt 0 \), maka \(2^{x} + 2^{-x} = \cdots\)
    1. \(\sqrt{2}\)
    2. \(\sqrt{5}\)
    3. \(\sqrt{7}\)
    4. \(\sqrt{10}\)
    5. \(\sqrt{11}\)
29. Diketahui \(x_{0}\) dan \(y_{0}\) adalah nilai-nilai yang memenuhi sistem persamaan \(\begin{cases}2^{x+1}-3^{y}=7 \\ -\left(2^{x-1} \right)-3^{y+1}=-5\end{cases}\)
    maka \(x_{0}+y_{0}\) adalah\(\cdots\)
    1. \(-1\)
    2. \(0\)
    3. \(1\)
    4. \(1\)
    5. \(2\)
30. Dalam basis 10, bilangan bulat positif \(p\) memiliki \(3\) digit, bilangan bulat positif \(q\) memiliki \(p\) digit, bilangan bulat positif \(r\) memiliki \(q\) digit. Nilai untuk terkecil untuk \(r\) adalah\(\cdots\)
    1. \(10^{10^{100}}\)
    2. \(10^{10^{100}-1}\)
    3. \(10^{10^{99}}\)
    4. \(10^{10^{99}-1}\)
    5. \(10^{99^{99}}\)
31. Hasil perkalian dari nilai \(x\) yang memenuhi \(\dfrac{x^{2}}{10.000}=\dfrac{10.000}{x^{2 \left({}^{10}\!\log x \right)-8}}\) adalah…
    1. \(10^{2}\)
    2. \(10^{3}\)
    3. \(10^{4}\)
    4. \(10^{5}\)
    5. \(10^{7}\)
32. Jika diketahui bahwa \(3^{(y-x)}(x+y)=1\) dan \((x+y)^{(x-y)}=3\), nilai \(x^{3y}=\cdots\)
    1. (1) \(-\frac{1}{9}\)
    2. (2) \(\frac{1}{9}\)
    3. (3) \(2\)
    4. (4) \(8\)
    1. (1), (2), dan (3), SAJA yang benar
    2. (1), dan (3), SAJA yang benar
    3. (2), dan (4), SAJA yang benar
    4. HANYA (4) yang benar
    5. SEMUA pilihan benar
33. Nilai dari \(\dfrac{1}{10^{-2017}+1}+\dfrac{1}{10^{-2016}+1}+\cdots+\dfrac{1}{10^{0}+1}+\cdots+\dfrac{1}{10^{2016}+1}+\dfrac{1}{10^{2017}+1}\) adalah…
    1. \(2015,5\)
    2. \(2017,5\)
    3. \(0\)
    4. \(1\)
    5. \(2017\)
34. Jika \(a_{1},a_{2},a_{3},\cdots,a_{n}\) adalah bilangan-bilangan asli berlainan yang memenuhi \(2^{a_{1}}+2^{a_{2}}+2^{a_{3}}+\cdots+2^{a_{n}}=2018\), maka nilai \(a_{1}+a_{2}+a_{3}+\cdots+a_{n}=\cdots\)
    1. \(44\)
    2. \(45\)
    3. \(46\)
    4. \(47\)
    5. \(48\)

About the Author

Math My Id

Administrator

Author's website Author's posts